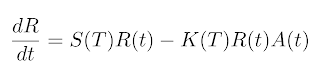For my first look at mathematical models, I thought I would see what happens when we put Metabolic Theory of Ecology, which predicts changes of organism metabolic related trait rates with temperature, together with classic predator-prey models! Sounds exciting, right?! I think so, mostly because predator prey models are interesting differential equation models by themselves and combing them with temperature dependence sounds cool. So, the question I'll be trying to answer is: what happens as temperature increases in predator-prey systems and can the systems go from stable to unstable populations? Another question I've stumbled across while working on this blogpost: why does blogger not support equations and why do my equations look terrible?
Short answer: With some temperature increases about the same as global warming, we see increasing instabilities in the predator-prey models. See the cool figure below and read the math for more information.
The Metabolic Theory of Ecology is one of the most surprising results of Ecology. In its strongest form, the one likely incorrect, it says that the activation energy for every metabolic process for every species on Earth is identically 0.66eV. That is quite surprising, to me at least, that the metabolic processes for an ant have the same activation energy as say, a human. Of course, this is empirical and not based on any actual theory of the chemistry or biology of metabolism. To learn more about it, check out this exhaustive data collection and analysis paper recently published in PNAS.Short answer: With some temperature increases about the same as global warming, we see increasing instabilities in the predator-prey models. See the cool figure below and read the math for more information.
The actual predictions that one can use from this model are the change in metabolic related traits as a function of temperature. Sooo, this metabolic theory of ecology can be applied to various animal models, like the predator-prey models. Let's make some Maths!
First, to introduce the Lotka-Volterra Equations, which is the name for predator-prey model I'll be using. Assume you have two populations: A(t), cats, and R(t), crows, with
Now we have everything to solve the linear system of ODEs and make them a function of temperature!
*Boring math I won't cover*
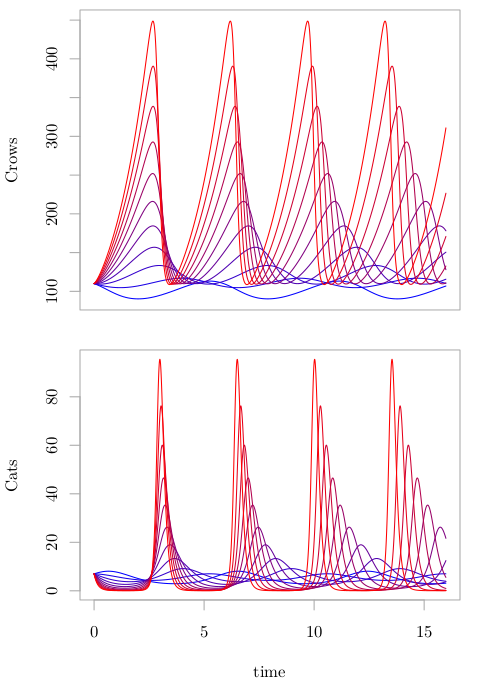
Phew! The solutions are plotted below. The populations as a function of time is plotted below. The color, from blue to red, is the temperature from 20 ℃ to 30 ℃.
There are a few interesting things to note here. The most visible change is the large increase in amplitude of the oscillations. This is a boon for the crows, apparently, because of their higher sexy time rate in the hot weather. Makes sense. For the cats, however, their death rate is increased and makes them much more susceptible to decreases in the crow population. This leads to strange behavior in the higher temperature at the cat minimums: 0.033 cats in some places! So, if 3 hundredths of a cat is unable to breed we'll have a problem at higher temperatures.
My conclusions: this MTE/Lotka-Volterra model predicts increases in the variation of species numbers which can lead to sudden extinctions. The model itself can't predict extinctions because it allows infinitesimal cats, but we can infer that a population of 33 millicats is extinction.
Let's assume that the crows are the prey and the cats are the predators. For the crows, they will have exponential growth minus the death from cats, which is proportional to the number of cats and crows (rate of "collisions'').
where S(T) stands for sexy time and is the growth rate. It is proportional to temperature according the MTE, because sexy time rate is a metabolic related trait! K(T) is the successful kill rate of crows by cats from an interaction. Now, for cats:
The same interaction term is here, but with the opposite sign. Cats reproduce after an entire crow. D(T) is the digestion rate or death rate, or something. The rate at which cats disappear which is offset by eating crows. The MTE predicts the following form for the metabolic terms:
where, as mentioned above, EA=0.66 eV. Now, where will those prefactors come from? D0 looks like some intrinsic cat property. However, if we know the D(T=T_i) at a certain value, we can find the D0 thanks to the universal activation energy. Also, we can find the D at a certain temperature given the equilibrium populations. Math is cool! Specifically, we can set the derivatives to 0 and find the equilibrium point.
Note, for you notation Nazis (if there is such a thing), I've dropped the function notation because I'm referring to a specific time and temperature. Now then, let's get some numbers. I looked outside this morning and it was 20℃. I counted 100 crows and 5 cats.
Ummm...well we're still unknown heavy. Ok, I'm going to start making assumptions now. Let's assume that K, the killing rate in familiar units of inverse square animals per time, is independent of temperature. I'll justify this by saying that aerobic processes are only considered to be temperature dependent in MTE. When cats and crows collide, it's all anaerobic action. So, that makes K a constant. If we think hard about K, we see it is the frequency at which one cat eats one crow (and then the cat has a baby). It clearly depends on the population density (area), but we'll just say in our world that a given cat and crow see each other up close once per week and the cat kills it once per 3 tries. That gives 1/21 (cat-crow-days)-1. That sets all the other constants.
 |
| Figure 1: Killing constant units of inverse cat-crows |
Solving the MTE Equation:
Now we have everything to solve the linear system of ODEs and make them a function of temperature!
*Boring math I won't cover*
Phew! The solutions are plotted below. The populations as a function of time is plotted below. The color, from blue to red, is the temperature from 20 ℃ to 30 ℃.
There are a few interesting things to note here. The most visible change is the large increase in amplitude of the oscillations. This is a boon for the crows, apparently, because of their higher sexy time rate in the hot weather. Makes sense. For the cats, however, their death rate is increased and makes them much more susceptible to decreases in the crow population. This leads to strange behavior in the higher temperature at the cat minimums: 0.033 cats in some places! So, if 3 hundredths of a cat is unable to breed we'll have a problem at higher temperatures.
My conclusions: this MTE/Lotka-Volterra model predicts increases in the variation of species numbers which can lead to sudden extinctions. The model itself can't predict extinctions because it allows infinitesimal cats, but we can infer that a population of 33 millicats is extinction.