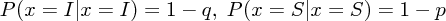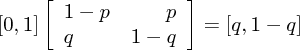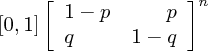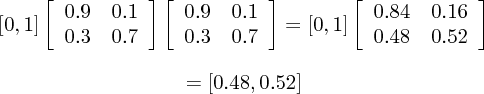Epidemiology has many interesting models for describing disease outbreaks. A large class of these models, the only ones with which I'm familiar in fact, are known as compartment models. One of the most amusing extensions of these models is incorporating a zombie compartment, or population. A researcher named Robert J. Smith? has developed some deterministic models for describing these zombie models. Not totally sure why he publishes with a question mark; I assume to differentiate his citation counts from all the other Robert Smiths. Anyway, his publications can be found here. It's interesting stuff, but I think I can do it with a stochastic version. In Part 1 of an unknown number, I'll introduce the SIS model and some matrix techniques for working with it. In Part 2, to be written, I'll move to Markov probability distributions instead of matrices and introduce zombies.
Stochastic vs. Deterministic
In a deterministic model, like the one I used in my first post, it is possible to subdivide populations into infinitesimal amounts. For example, in some of Mr. Smith?'s models, he ran into problems where no strategy could wipe out the zombies because even fractional amounts of a zombie can cause a zombie-Apocalypse. That didn't seem to prevent his research paper from being highlighted in hundreds of news articles, including Wired. If, however, we formulate this into a stochastic model, there are two advantages. First, it is discrete, so that we may only have 1 or 0 or 10 zombies. Second, the model is in a probability framework, so we may estimate the probability that the zombies win, as opposed to deterministic models where the zombies win or lose every time.
SIS Model
The susceptible-infected-susceptible (SIS) model is a simple compartmental model to practice with and develop the techniques necessary to analyze more complicated models. The basic definition is that there are two populations, the infected and susceptible and the probability of being infected is constantly p and the probability of being cured is constantly q. Formally:
Notice that p and q do not necessarily sum to 1. If they do, the model simplifies a lot, or as I call it, becomes incredibly boring. You stochastic modelling superstars will recognize that case as the doubly stochastic.
SIS Model
The susceptible-infected-susceptible (SIS) model is a simple compartmental model to practice with and develop the techniques necessary to analyze more complicated models. The basic definition is that there are two populations, the infected and susceptible and the probability of being infected is constantly p and the probability of being cured is constantly q. Formally:
Notice that p and q do not necessarily sum to 1. If they do, the model simplifies a lot, or as I call it, becomes incredibly boring. You stochastic modelling superstars will recognize that case as the doubly stochastic.
SIS Matrix Model
Let's begin with a single individual with two states, state S and I. This can be encoded into a vector like so:
Let's begin with a single individual with two states, state S and I. This can be encoded into a vector like so:
That vector will be called the state vector because it represents the state of our model. In this case, it says the individual is infected. We can then represent the probabilities of going from state S to I, state S to S, etc. into a transition probability matrix:
This formalism has some cool advantages. For example, if we know where we are, i.e. have a vector encoding our state, we can calculate the probabilities of being infected or susceptible using matrix multiplication:
Note how the matrix multiplication is exactly what we expect, that the probability of being susceptible after being infected is q and remaining infected is 1 - q. Further, we can repeat that to find the probability of being in both states after a n steps:
For a concrete example, let's find the probability that our individual is infected in two steps, given that he starts as infected and that the probability of being infected is 10% and the probability of being cured (infected to susceptible) is 30%:
So, the probability of infection is 52%. As I should note, in this simple case, no matter where we begin, after a "very long" time, the probability of being in each state is constant. This is called the stationary distribution. These probabilities can be found by solving the left-handed characteristic equation on the transition probability matrix. Students of stochastic modelling are always trying to find the stationary distribution. In any case, the matrix framework has some excellent advantages, like the matrix multiplication for finding probabilities into the future and the well-defined method for finding stationary distribution (provided it exists!).
This formalism has some cool advantages. For example, if we know where we are, i.e. have a vector encoding our state, we can calculate the probabilities of being infected or susceptible using matrix multiplication:
Note how the matrix multiplication is exactly what we expect, that the probability of being susceptible after being infected is q and remaining infected is 1 - q. Further, we can repeat that to find the probability of being in both states after a n steps:
For a concrete example, let's find the probability that our individual is infected in two steps, given that he starts as infected and that the probability of being infected is 10% and the probability of being cured (infected to susceptible) is 30%:
So, the probability of infection is 52%. As I should note, in this simple case, no matter where we begin, after a "very long" time, the probability of being in each state is constant. This is called the stationary distribution. These probabilities can be found by solving the left-handed characteristic equation on the transition probability matrix. Students of stochastic modelling are always trying to find the stationary distribution. In any case, the matrix framework has some excellent advantages, like the matrix multiplication for finding probabilities into the future and the well-defined method for finding stationary distribution (provided it exists!).
SIS Big Matrix
Let's see how well the matrix formalism holds up to larger systems, where there is more than one individual. Let's start with two individuals. Our state vector now needs to encode two individuals. No problem, we just add a column:
Person 1 (top row) is infected and person 2 (second row) is susceptible. Simple! Now, let's see what the probability of infection is for each person is after two steps:
Matrices rule! Now, what happens when we want to encode 100 individuals? Feasible, but we'll need to use a computer to deal with a 100 column matrix. What about the United States? Well, now we are running into trouble... Next post I'll show how to deal with this problem by assuming each individual is indistinguishable and how to put zombies in your math.
Person 1 (top row) is infected and person 2 (second row) is susceptible. Simple! Now, let's see what the probability of infection is for each person is after two steps:
Matrices rule! Now, what happens when we want to encode 100 individuals? Feasible, but we'll need to use a computer to deal with a 100 column matrix. What about the United States? Well, now we are running into trouble... Next post I'll show how to deal with this problem by assuming each individual is indistinguishable and how to put zombies in your math.