In this post, I'll mention briefly some places to look for polymer physics information and the systems I'm studying.
So I had this hope when beginning to study polymer physics that they would have already completed analytic treatment of the problems which I'm interested in. I was in particularly interested in seeing the scaling behavoir for single polymers in spherical confinement as well as analytical treatment of random copolymers in spherical confinement. There has been quite a bit of interesting work on analytical polmyer physics. A nice place to start is Scaling Concepts in Polymer Physics by Pierre-Gilles de Gennes. That book is definitely good if you're interested in scaling behavoir and approximations of polymer systems. More modern work is largely based on a fascinating connection between path integrals in quantum mechanics and path integrals of polymers. Modern polymer physics theory is particularily interesting because some beautiful approaches to mean-field theory have been developed. For example, take a look at this paper by M. Schick, http://pubs.acs.org/doi/abs/10.1021/ma9717505, which shows how mean-field theory approximations are used in polymer physics, in this case tethered polymers on a surface.
The problem I'm interested in has not quite been treated well enough for analytical results. I'm very curious about a type of confinement sometimes known as "strong confinement", which means that the macromolecule are confined in a sphere. The strong part is because there is no dimension which the macromolecule can extend in. In slit confinement, for example, there is the dimension parallel to the slit into which the polymer can extend. This distinction is important for expressions of the free energy, which is typically extensive like in the slit case. In a sphere, this isn't the case because there is literally a finite volume for the molecules to fit into.
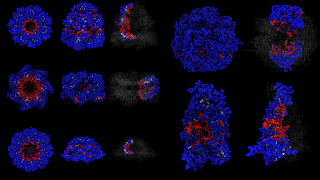
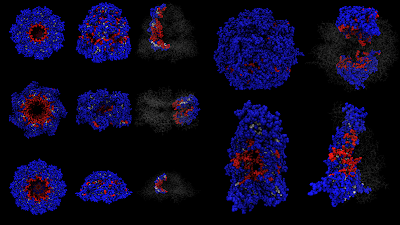
The actual system I'm studying is molecular chaperones, some of which are shown below. They aren't strictly spherical shapes, but they all strongly confine a protein (biological macromolecule) inside of them. These molecular chaperones assist protein folding. Proteins are encapsulated in the chaperones, which are themselves huge complexes made up of dozens of proteins, and the proteins are able to fold inside the chamber. These protein complexes, the chaperones, are between 50-100 angstroms in diamter. I've been studying them briefly for a side project related to some of my bioinformatics work on protein surfaces.
There is some theoretical work on strong confinement, but very little on random copolymers, which are models of proteins. There is some work though on single component polymers. I'm not going to post any results today; maybe once I finish writing the work for publication I'll post some stuff on the blog. I'll leave you with a picture of some preliminary work. I and my research assistant developed a computational geometry method to determine which residues are in the interior cavity, which are buried, and which are on the exterior surface. That is what the colors represent.