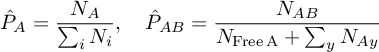Amino Acid Interactions

I couldn't find a nice table of amino acid interaction energies, so I created one from crystallography data of thousands of protein. Here are the results and an explanation of how I did it. There is also a black and white version in the article which could be nice for printing. I don't know, I printed a pdf but blogger won't host pdfs for me.
I've been working with protein modelling in my research lately and I love how computer science-y the field is. There is an "alphabet" of amino acids and they can be categorized by type (e.g, hydrophilic, aromatic). There are hierarchical structures to proteins: primary, secondary, tertiary which are dictated by interactions from the alphabet of amino acids. It's all so well ordered and things fit neatly together. Of course, there are messy bits to practical studies of proteins like glycosilation, signaling peptides, coordinating metals and other little things that can complicate protein simulations and experiments. Overall, though, the concepts are much more structured than other areas I study.
One thing which I've not really seen is a cheat sheet of amino acid-amino acid interactions. There are general rules, like positively charged amino acids bind to negatively charged amino acids. However, there isn't a nice chart of which interactions are strongest or which are disfavored etc. So I've decided to create one according to the following simple recipe:

1. Create a database of 3-dimensional protein structures.
2. Tabulate the number of times each amino acid type is in contact with another amino acid type.
3. Turn the counts into interaction energies.

This is a relatively simple task, I mean relative to other research I do but not necessarily easy. Let's look at step 1. Protein structures may be found at the protein data bank. It is simple to download a collection of structures from there. A few little things should be done though, like ensuring the structures aren't too similar and they aren't missing pieces. Overall though, obtaining the structure is not so hard.
For step 2, tabulating the contacts requires some definition of a contact. This is somewhat arbitrary, but I'll use Van der Waals distances which are come from a theory of molecular interactions. Each pair of atom types, for example nitrogen near oxygen, has some critical distance below which the pair will be considered "in contact." That covers atoms, however we're discussing amino acids which are molecules made up of many atoms. Thus, I'll consider two amino acids to be in contact if any two of their atoms are in contact with one another. This allows me to tabulate contacts. There are a few small details which must be considered, like ignoring hydrogens, which are small enough to be neglected, and to ignore contact between neighboring residues. The justification for ignoring neighboring residues is that it is relatively easy for neighboring residues to be in contact because the definition of contact is somewhat weak (any two atoms in contact), and thus I'll err on the side of being conservative for the number of contacts. This shouldn't introduce any systematic bias. What will introduce systematic bias though is the Van der Waals radii. Having the carbon radius, for example, as too small could under estimate the hydrohpobic force which brings carbon rich amino acids together.
At this point, I have a matrix containing the number of contacts between all 20 amino acids, creating a symmetric 400 element matrix. In order to convert this into interaction energies, I'll need to assume some sort of probability model. I believe it is fairly intuitive that there will be two type of parameters in this model: the probability of observing residue A and the probability that residue A is in contact with residue B. More formally, our data consists of a series of 2 observation length Markov chains and we'd like to estimate the initial distribution and the transition probabilities. These are simple enough:
where N is the number of observations, either of the number of residues of type A or of contacts between A and B. 'Free' here indicates residues which are not in contact.
Now to covert these statistics into interaction energies I'll use the Boltzmann distribution, which connects energies and probabilities. I think there's some other term for this business in statistical modelling, like Gibbs random fields or something, but anyway we can use the following equations to get energies, beginning with Χ, the interaction energy.
U is the energy of a pair contact and k is the energy scale, generally taken to be Boltzmann's constant. This definition of interaction energy can be thought of as the contact energy relative to a reference state where the two amino acids involved in the contact are infinitely far away.
Now it is possible to put everything together. I'll leave the temperature unspecified and thus my units will be in kT. For those of you confused about all these equations, all I did was estimate the probabilities from the data and took the negative natural logirthm of the probabilities. Simple. Now, I'll plot the results and we'll see how closely the interaction energies match our intuition.
The "Ar", "Po", "Ch", and "Hy" abbrievations stand for aromatic, polar, charged, and hydrophobic, respectively. Red indicates a strongly favored interaction and blue is a strongly disfavored interaction. I've also created a black and white version, below, which will go nicely on the wall next to my other cheat sheets of amino acid information. The cysteine-cysteine pair is excluded because their interaction is covalent. The rest of the interactions do match what we would expect. Positvely charged residues contact negatively charged residues. Hydrophobic residues dislike polar residues. Aromatics bind strongly. The chart came out quite nice in fact!
There is one issue which may require improvement, however. The charged residues seem to interact with one another much more strongly than the hydrophobic residues interact with themselves. This is indeed possible, but I don't know if anyone has experimental evidence that a salt bridge (negatively charged amino acid in contact with a positively charged amino acid) is nearly twice as strong as a hydrophobic contact. In fact, there has been research showing the opposite. This discrepancy, I believe, is from the systematic bias I was worried about in the Van der Waals radii. The good news is that if I ever do find experimental evidence giving a few quantitative interaction energies, I can go back to fit the Van der Waals radii and thus create a more accurate table.